https://www.acmicpc.net/problem/2565
2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
문제
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.
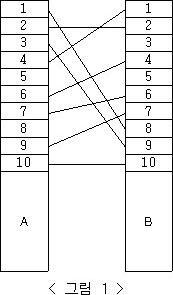
전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는 위치의 번호가 차례로 주어진다. 위치의 번호는 500 이하의 자연수이고, 같은 위치에 두 개 이상의 전깃줄이 연결될 수 없다.
출력
첫째 줄에 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 출력한다.
접근법
작게 축소해서 한번 보자

무작위로 그린 그림이다. 위 그림에서 당연하게도 1-5와 5-3을 지워야할 것처럼 보인다.
왼쪽이 정렬되어있다는 가정하에 오른쪽만 주시해보자.
왼쪽을 기준으로 오른쪽을 나열하면
5 1 2 4 3 이다.
최대한 겹치는 전깃줄을 고르려고 노력해보았다. 당연히 숫자가 크면 그만큼 겹치는 전기줄이 있을 수 있다. 하지만 겹치지 않는 경우도 존재하기 때문에 이 방법은 포기했다.
( 3-8, 1-1, 2-2 인 경우 겹치지 않는다. )
그래서 반대로 겹치치 않는 전기줄을 전체에서 빼면 좋을 것 같다고 생각했다.
겹치지 않는 전기줄(i)은 이전의 전기줄(j) 보다 오른쪽 수가 작아야한다.

위 그림에서 i=2인 전기줄의 오른쪽은 1이다.
따라서 j=1의 오른쪽(5)이 1보다 크기 때문에 해당 전깃줄(j)는 제거해야하는 전깃줄이 된다.
이 말을 다시 생각해보면, i=N의 전깃줄에 대해 j가 작아야 하므로
가장 긴 증가하는 부분 수열을 구하는 것과 같은 원리임을 알 수 있다.
그러므로 위 예시에서 5 1 2 4 3 의 가장 긴 증가하는 부분 수열은
1 2 3 이므로 제거하지 말아야할 전기줄은 3,
결과적으로 제거해야할 전깃줄은 전체(5) - 3 = 2 이다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define MAX 501
vector <pair<int, int>> v;
int dp[MAX];
int main() {
int n;
cin >> n;
// 전깃줄이 1번부터 시작해서 0은 더미 데이터로 넣는다.
v.push_back({ 0,0 });
for (int i = 0; i < n; i++) {
int a, b;
cin >> a >> b;
v.push_back({ a,b });
}
// 왼쪽 기준 정렬
sort(v.begin(), v.end());
int res = 0;
for (int i = 1; i <= n; i++) {
dp[i] = 1;
for (int j = 1; j < i; j++) {
// 자신보다 전의 전깃줄이 작아야함 (오른쪽)
if (v[j].second < v[i].second) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
// 없애지 말아야할 전깃줄 최대값
res = max(res, dp[i]);
}
cout << n-res;
}

'📊알고리즘 > BOJ' 카테고리의 다른 글
| [BOJ 1786] 찾기 (0) | 2023.08.22 |
|---|---|
| [👊DP뿌시기 #10] (BOJ 9215) LCS (0) | 2023.08.21 |
| [👊DP뿌시기 #8] (BOJ 11054) 가장 긴 바이토닉 부분 수열 (0) | 2023.08.20 |
| [👊DP뿌시기 #7-2] (BOJ 11722) 가장 긴 감소하는 부분 수열 (0) | 2023.08.20 |
| [👊DP뿌시기 #7] (BOJ 11053) 가장 긴 증가하는 부분 수열 (0) | 2023.08.20 |

