https://www.acmicpc.net/problem/9251
9251번: LCS
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net
문제
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
입력
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
출력
첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.
브루트포스로 그냥 무식하게 구할 수 있다. 그러나 이를 DP를 이용해보자.
LIS는 수열 내에서 이루어졌다면, LCS는 두 문장을 서로 비교해야한다.
하나의 문자에 대해 총 2가지 경우가 있다.
1. 해당 문자를 포함하는 경우
2. 해당 문자를 포함하지 않는 경우
위 두 경우를 어떻게 이용할까?
일단 dp 테이블을 정의하자
두 문자열 a,b에 대해
DP[i][j] = i번째 까지 b 문자열(b[0] ~ b[i])과 j번째까지 a 문자열(a[0] ~ a[j])의 LCS(z[k])
각 문자열의 마지막인 b[i]와 a[j]를 나누면
1. b[i] == a[j]
2. b[i] != a[j]
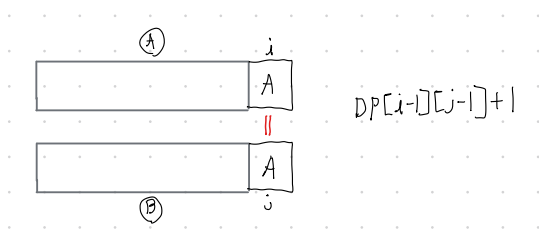
b[i] == a[j]의 경우는 각각의 b[i]와 a[j]가 포함되는 경우이다.
공통 부분 수열인 Z에 b[i]와 a[j]가 포함되므로 당연하게
b[i-1]과 a[j-1] 의 공통 부분 수열인 DP[i-1][j-1]에 +1을 한것이다.
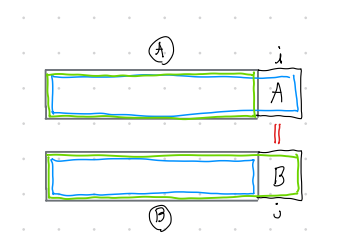
두번째 경우인 B[i] != A[j]는 두 문장 모두 포함되지 않으므로 둘 중 하나만 포함된다.
근데 B[i] 와 A[j] 중 어떤 것이 포함되는지 알 수 없다.
따라서 우리는 둘 중 LCS가 더 큰 값을 가져오면 된다.
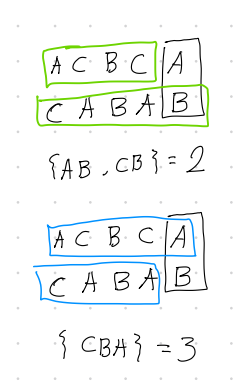
예를 들어 위와같이 끝 문자가 A, B로 다를 때, A를 포함한 LCS가 더 크기에 우리는 A를 포함하도록 해야한다.
위 두 가지를 고려해서 점화식을 세우면 다음과 같다.
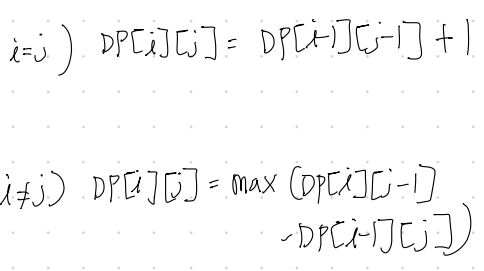
최종적으로 예시의 DP Table을 그려보면 이렇다.

코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define MAX 1001
int dp[MAX][MAX];
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
string a, b;
cin >> a;
cin >> b;
int aLen = a.length();
int bLen = b.length();
int res = 0;
for (int i = 1; i <= bLen; i++) {
for (int j = 1; j <= aLen; j++) {
if (a[j-1] == b[i-1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
cout << dp[bLen][aLen];
}
같이보기
'📊알고리즘 > BOJ' 카테고리의 다른 글
| [👊DP뿌시기 #11] (BOJ 12865) 평범한 배낭 (0) | 2023.08.23 |
|---|---|
| [BOJ 1786] 찾기 (0) | 2023.08.22 |
| [👊DP뿌시기 #9] (BOJ 2565) 전깃줄 (1) | 2023.08.21 |
| [👊DP뿌시기 #8] (BOJ 11054) 가장 긴 바이토닉 부분 수열 (0) | 2023.08.20 |
| [👊DP뿌시기 #7-2] (BOJ 11722) 가장 긴 감소하는 부분 수열 (0) | 2023.08.20 |


