모두 Divide and Conquer로 구현 가능하다.
Recursion을 이용해서 구현해보자.
합병 정렬
기본 개념
1. 하나의 리스트를 두 개의 리스트로 분할 (리스트 사이즈가 2일 때까지)
2. 분할된 리스트를 각각 순회하면서 작은 순서대로 새로운 리스트에 추가
3. Recursion을 빠져나오면서 정렬된 리스트들끼리 계속 2번 진행
4. 최종적으로 정렬된 리스트를 반환

의사코드
Alg mergeSort(list L)
if(L.size > 1)
// divide
L1, L2 = partition(L)
// recursion
L1 = mergeSort(L1)
L2 = mergeSort(L2)
// Conquer
L = merge(L1, L2)
return L
merge
Alg merge(L1, L2)
L = new List
while(!L1.isEmpty & !L2.isEmpty)
if(L1[0].data < L2[0].data)
L.add(L1[0])
removeFirst(L1)
else
L.add(L2[0])
removeFirst(L2)
while(!L1.isEmpty)
L.add(L1[0])
removeFirst(L1)
while(!L1.isEmpty)
L.add(L1[0])
removeFirst(L1)
return LC 구현
구현을 위해서 Devide, Recursion, Conquer 총 세 부분으로 나눠서 구현해보자.
List* mergeSort(List* l) {
List** listArr = NULL;
if (l->size > 1) {
// 1. Divide
listArr = partition(l, l->size / 2);
// 2. Recursion
listArr[0] = mergeSort(listArr[0]);
listArr[1] = mergeSort(listArr[1]);
// 3. Conquer
l = merge(listArr[0], listArr[1]);
}
return l;
}- 재귀로 진행되기 때문에, 정렬된 리스트가 return l로 반환되면 호출한 메서드의 listArr[0]에 l이 들어간다.
Partition
List** partition(List* l, int size) {
List** listArr = (List**)malloc(sizeof(List*) * 2);
listArr[0] = buildList();
listArr[1] = buildList();
listArr[0]->size = size;
listArr[1]->size = l->size - size;
// Start, end point
Node* l1_start = NULL;
Node* l1_end = NULL;
Node* l2_start = NULL;
Node* l2_end = NULL;
// Point setting
l1_start = l->header->next;
l1_end = findNodeAtIndex(l, size);
l2_start = l1_end->next;
l2_end = findNodeAtIndex(l, l->size);
// Insert point to list
listArr[0]->header->next = l1_start;
l1_end->next = listArr[0]->trailer;
listArr[1]->header->next = l2_start;
l2_end->next = listArr[1]->trailer;
free(l);
return listArr;
}- 파티션은 단순하게 나누는 과정이므로 쉽게 구현이 가능하다.
Merge(Conquer)
List* merge(List* l1, List* l2) {
List* res = buildList();
Node* resN = res->header;
Node* n1 = l1->header->next;
Node* n2 = l2->header->next;
while (n1 != l1->trailer && n2 != l2->trailer) {
if (n1->data > n2->data) {
resN = addLastNode(resN, n2->data);
n2 = n2->next;
}
else{
resN = addLastNode(resN, n1->data);
n1 = n1->next;
}
res->size++;
}
while (n1 != l1->trailer) {
resN = addLastNode(resN, n1->data);
n1 = n1->next;
res->size++;
}
while (n2 != l2->trailer) {
resN = addLastNode(resN, n2->data);
n2 = n2->next;
res->size++;
}
resN->next = res->trailer;
return res;
}
시간 복잡도
재귀 호출 시, 리스트가 절반이 되기 때문에
트리의 높이: O(logN)
노드를 내려갈때 마다 리스트의 크기가 2^i개의 N/2^i로 나뉘기 때문에
깊이 별 노드 작업량: O(N)
따라서, 전체 시간복잡도: O(N logN)
퀵 정렬
기본 개념
1. 피벗을 정한다.
2. 피벗을 기준으로 피벗보다 작은 부분, 피벗보다 큰 부분, 피벗과 같은 부분 으로 나눈다.
3. 리스트의 사이즈가 1보다 클 동안 2번을 반복한다.
4. 아까전에 나눈 세 부분은 이미 정렬되어 있기 때문에, 순서대로 합치면 된다.

의사코드
Alg quickSort(L)
if (L.size() > 1)
k = a position in L
Less, Eql, Grt = partition(L, k)
quickSort(Less)
quickSort(Grt)
L = merge(Less, Eql, Grt)
return LAlg partition(L,Pivot)
p = L.get(Pivot) // pivot 값 저장
LT, EQ, GT = empty list
while (!L.isEmpty())
e = L.removeFirst()
if (e < p)
LT.addLast(e)
elseif (e = p)
EQ.addLast(e)
else {e > p}
GT.addLast(e)
return LT, EQ, GT- Pivot을 기준으로 작고, 같고, 큰 부분을 나눠서 리스트로 만든다,
- 이미 구분을 했기 때문에 merge는 순서대로 삽입만 하면된다.
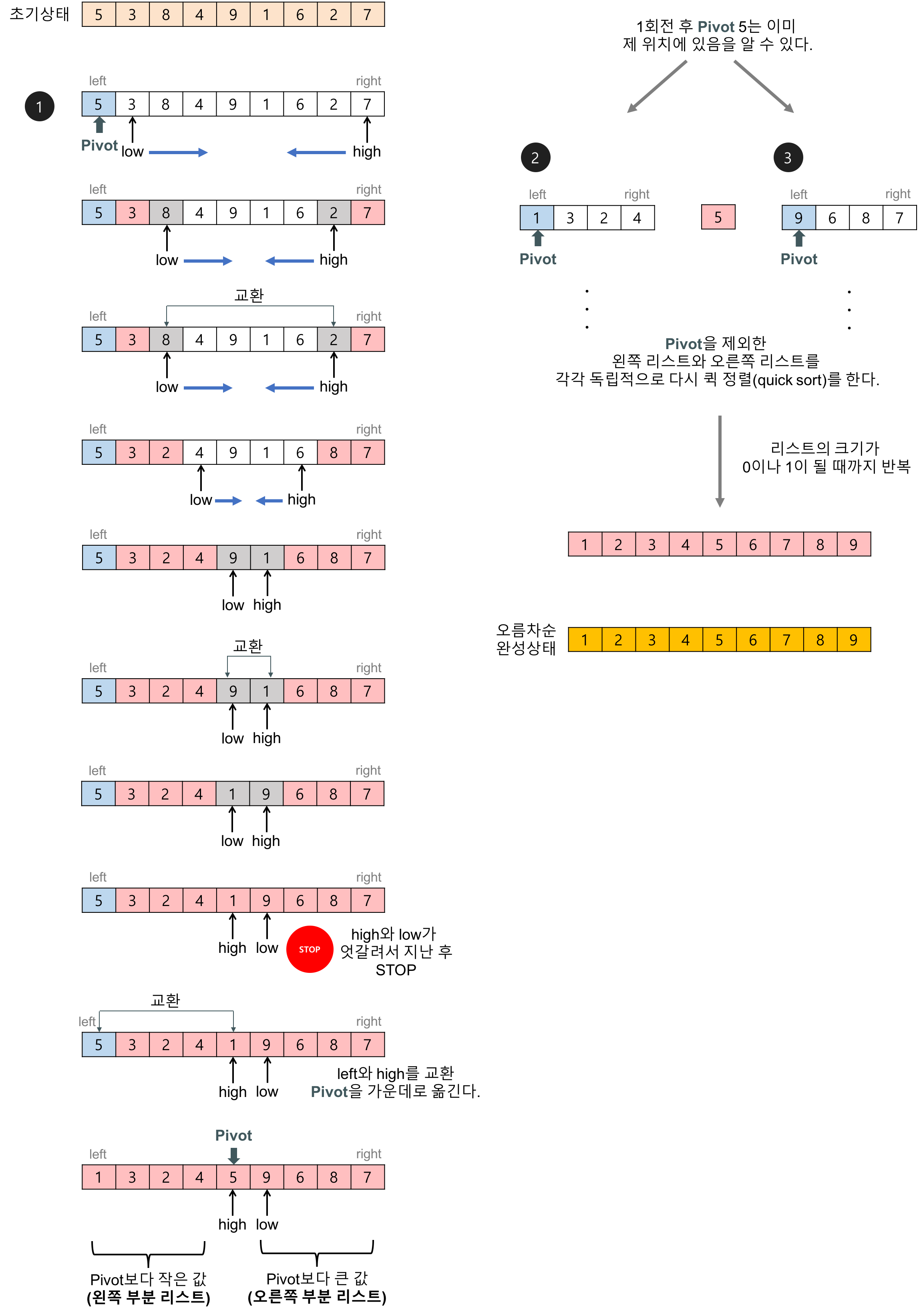
퀵정렬 예시
[파티션 과정]
1. 양끝을 l, r로 둔다.
2. l은 +1, r은 -1하면서 l값 > r값 이면 서로 Swap한다.
3. l > r이면 멈춘다. (전체를 다 돌았기 때문)
4. 피벗 위치를 반환한다.
시간 복잡도
최악
Pivot이 항상 최소이거나 최대일 때, O(N^2)
투포인터이기 때문에 평균 파티션 속도는 O(N/2)이지만,
Pivot이 항상 최소이거나 최대이면 O(N-1)이 걸린다.
따라서, 깊이 n-1 * 깊이별 O(N-1) = O(N^2)
따라서, Pivot위치가 실행 시간을 결정한다.
크기 s인 리스트에 대해 Less와 Grt의 크기가 모두 (3/4)s 일때 좋은 호출이라고 가정한다.
무작위 Pivot에 대한 시간 복잡도
좋은 호출의 리스트 크기: (3/4)^(i/2)
기대 높이: O(logN)
각 깊이의 작업량: O(N)
따라서, O(N logN)
합병 정렬 vs 퀵 정렬
| 합병 정렬 | 퀵 정렬 | |
| 구현 | 분할정복 | 분할정복 |
| 시간 복잡도 | 최악: O(N logN) | 최악: O(N^2) 기대: O(N logN) |
| Divide vs. Conquar | 분할 쉬움 합병 어려움 (서로 비교) |
분할 어려움 (세 부분 분할) 합병 쉬움 |
| inPlace | 어려움(두개로 분할) | 쉬움 (예제 활용) |
| 작업 순서 | 작은 것 -> 큰 것 | 큰 것 -> 작은 것 |
'🏫학부 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최소신장트리 (작성중) (0) | 2023.11.23 |
|---|---|
| [알고리즘] 방향그래프 (0) | 2023.11.21 |
| 이진탐색트리 (0) | 2023.10.08 |

