방향그래프
- 모든 간선이 방향간선
방향그래프의 속성
- 모든 간선은 한 방향으로만
- G가 단순(간선이 많지 않음) : M <= N(N-1)
- 진입간선, 진출간선을 인접리스트로 이용 시, 크기에 비례해 조사 가능
방향 DFS
- DFS와 BFS를 방향그래프로 표현 가능
- 트리간선, 후향간선, 전향 간선, 교차간선

1. 트리간선: 자식을 가리키는 기본적인 간선
2. 후향간선: 조상을 가리키는 간선
3. 전향간선:
4. 교차간선
도달가능성
u->v인 방향경로가 존재하면, "u는v에 도달한다" , "v는 u로부터 도달 가능하다"
강연결성
어느 두 정점 u, v 간에 u에서 v 도달가능 이고 v에서u 로 도달가능이면 강연결
강연결 검사 알고리즘
1. 임의 정점 v 선택
2. v에서 DFS 실행
3. 간선들 방향을 역행시킨 그래프 G'을 얻음
4. G'에서 v에서부터 DFS 수행
-> O(n+m)
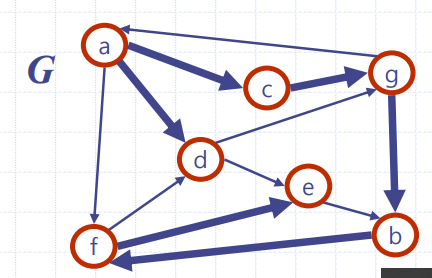

강연결 요소
- 최대한 모든 정점을 도달할 수 있는 부그래프

a->f로 간다고 하면, a로 다시 올 수 없음.
이행적폐쇄
다음 성질을 만족.
1. G'은 G와 동일한 정점들로 구성
2. G의 u에서 v(v!=u)로의 경로가 존재하면 u에서 v로의 방향간선을 추가해줌.
한줄: v에서 u로의 경로가 존재하면 도달가능하다는 간선을 추가해줌.
방향그래프에 관한 도달 가능성 정보를 제공하는 것임.
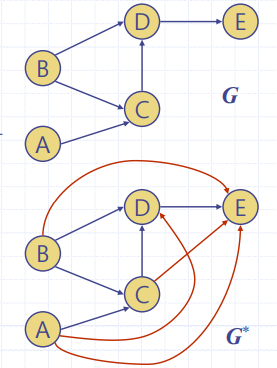
이행적폐쇄 계산
[ 방법 ]
1. 각 정점에서 DFS 수행
-> O(n(n+m)) : n * (n+m) = 총 정점 * DFS
2. 플로이드-와샬 알고리즘 (DP)
플로이드-와샬 이행적폐쇄
1. 정점을 1~n까지 번호 매김
2. 1~n까지 Loop 돌면서 k를 경유 정점으로 쓰는 경로를 고려

[ 의사 코드 ]
Alg Floyd-Warshall(G)
G[0] <- G
for k<-1 to n
G[k] <- G[k-1]
for i <-1 to n, i!=k
for j<-1 to n, j!=i,k
if(G[k-1].are Adjacent(v[i], v[k])
&& G[k-1].areAdjacent(v[k],v[j]))
if(!G[k].areAdjacent(v[i],v[j]))
G[k].insertDirectedEdge(v[i],v[j],k)
return G[n]
동적 프로그래밍
[ 조건 ]
- 부문제 단순성 : 부문제들이 몇 개의 변수로 정의될 수 있는 경우
- 부분제 최적성 : 전체 최적치가 최적의 부문제들에 의해 정의될 수 있는 경우
- 부문제 중복성 : 부문제들이 독립적이 아니라 상호 겹쳐질 경우 (상향식으로 구축되야함)
## DP vs. Divide And Conqual
| DP | 분할통치법 | |
| 공통점 | 원점 - 목표점 구조 원점: 문제의 초기 또는 기초 지점 목표점: 최종해가 요구되는 지점 |
|
| 차이점 | 원점 -> 목표점 (단방향) | 목표점 -> 원점 -> 목표점(양방향) (단 해를 구하기 위한 연산 진행은 원점 -> 목표점) |
| 성능 | 단방향 때문에 종종 효율적 | 분할 회수 및 중복연산 수행 회수 |
방향 비싸이클 그래프 (DAG)
: 방향싸이클이 존재하지 않는 방향그래프

## DAG와 위상정렬
- 방향그래프의 위상순서
: 모든 i<j인 간선(v[i], v[j])에 대해 정점들을 번호로 나열
- 방향그래프가 DAG면 위상순서를 가지며, 그 역도 참!
위상 정렬
: DAG로부터 위상순서를 얻는 절차
정점의 진입차수 이용하는 위상 정렬
[ 의사 코드 ]
Alg topologicalSort(G)
forEach u <- G.vertices()
//in[u]: u의 진입차수
in[u] <- u.inDegree
// 진입차수가 0 이면 enque
if(in[u] == 0)
Q.enqueue(u)
// 위상정렬 인덱스
i<-1
while(!Q.isEmpty())
// 진입차수 0인 정점 큐에서 가져옴
u<-Q.dequeue()
i<-i+1
// u에서 나가는 간선돌림
forEach e<-G.outIncidentEdges(u)
// 도착 간선을 가져와서 진입차수를 -1함
w<-G.opposite(u,e)
in[w] <- in[w] - 1
// 진입차수 0되면 큐에 넣음
if(in[w] == 0)
Q.enqueue(w)
// 위상정렬 인덱스가 모든 정점에 매겨지지 않으면 사이클 있다고 알림
if(i<=n)
write("G에서 사이클 발견!")
return
DFS를 특화한 위상 정렬
[ 의사 코드 ]
Alg topologicalSortDFS(G)
n <- G.verticeCount
forEach u<-G.vertices()
l(u) <- Fresh
forEach v<-G.vertices()
if(l(v) == Fresh)
rTopologicalSortDFS(G,v)
returnAlg rTopologicalSortDFS(G,v)
l(v)<- Visited
forEach e<-G.outIncidentEdges(v)
w<-opposite(v,e)
if(l(w) == Fresh)
rTopologicalSortDFS(G, w)
else if ("w 가 위상정렬로 번호 안메겨졌으면")
write("그래프에서 싸이클 발견")
v를 n으로 번호매김
n<-n-1
위상 정렬 알고리즘 분석
두 갭의 버전 모두
시간복잡도: O(n+m)
공간복잡도: O(n)
'🏫학부 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최소신장트리 (작성중) (0) | 2023.11.23 |
|---|---|
| 이진탐색트리 (0) | 2023.10.08 |
| 합병 정렬과 퀵정렬 (0) | 2023.10.04 |

