https://www.acmicpc.net/problem/4883
4883번: 삼각 그래프
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이
www.acmicpc.net
문제
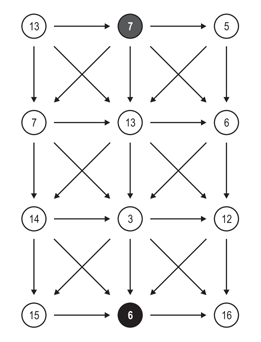
이 문제는 삼각 그래프의 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최단 경로를 찾는 문제이다.
삼각 그래프는 사이클이 없는 그래프로 N ≥ 2 개의 행과 3열로 이루어져 있다. 삼각 그래프는 보통 그래프와 다르게 간선이 아닌 정점에 비용이 있다. 어떤 경로의 비용은 그 경로에서 지나간 정점의 비용의 합이다.
오른쪽 그림은 N = 4인 삼각 그래프이고, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 경로 중 아래로만 가는 경로의 비용은 7+13+3+6 = 29가 된다. 삼각 그래프의 간선은 항상 오른쪽 그림과 같은 형태로 연결되어 있다.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이 순서대로 주어진다. 비용은 정수이며, 비용의 제곱은 1,000,000보다 작다.
입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최소 비용을 테스트 케이스 번호와 아래와 같은 형식으로 출력한다.
접근법
그래프를 보고 단순하게 해결할 수 있는 문제이다.
여기서 주의할 점은 첫번째 줄 2번째에서 시작한다는 것이다.
DP[i][j]를 i번째 행의 j번째 노드 까지의 최소 비용으로 정의하면,
DP[2][1]과 DP[2][2]에 대해서 따로 정의해줘야한다.
나머지 노드들은 그래프와 같이
i) j==1
dp[i][j] = min(dp[i - 1][j + 1], dp[i - 1][j]);
ii) j==2
dp[i][j] = min(dp[i][j - 1],
min(dp[i - 1][j], min(dp[i - 1][j + 1],dp[i - 1][j - 1])));
iii) j==3
dp[i][j] = min(dp[i][j - 1],
min(dp[i - 1][j - 1], dp[i - 1][j]));
이렇고, dp[i][j]+=arr[i][j]를 한것과 같다.
그러나 위에서 처럼 DP[2][1]은 DP[1][1]에서 오는 것을 제외해야한다.
마찬가지로 DP[2][2]도 DP[1][1]에서 오는 것을 제외해야한다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cmath>
#define MAX 100001
using namespace std;
int n,x;
int arr[MAX][4];
int dp[MAX][4];
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int a, b, c;
for (int idx = 1;;idx++) {
cin >> n;
if (n == 0) break;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= 3; j++) {
cin >> arr[i][j];
dp[i][j] = 0;
}
}
dp[1][2] = arr[1][2];
dp[1][3] = dp[1][2] + arr[1][3];
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= 3; j++) {
if (j == 1) {
if(i==2)
dp[i][j] = dp[i - 1][j + 1];
else
dp[i][j] = min(dp[i - 1][j + 1], dp[i - 1][j]);
}
else if (j == 2) {
dp[i][j] = min(dp[i][j - 1],
min(dp[i - 1][j], dp[i - 1][j + 1]));
if (i != 2)
dp[i][j] = min(dp[i - 1][j - 1], dp[i][j]);
}
else {
dp[i][j] = min(dp[i][j - 1],
min(dp[i - 1][j - 1], dp[i - 1][j]));
}
dp[i][j] += arr[i][j];
}
}
cout << idx << ". "<<dp[n][2] << '\n';
}
}
'📊알고리즘 > BOJ' 카테고리의 다른 글
| [DP #21] (BOJ 2011) 암호코드 (0) | 2023.09.01 |
|---|---|
| [DP #20] (BOJ 10942) 팬린드롬? (0) | 2023.08.31 |
| [DP #18] (BOJ 2482) 색상환 (0) | 2023.08.30 |
| [DP #17] (BOJ 15486) 퇴사 2 (0) | 2023.08.29 |
| [👊DP뿌시기 #13-2] (BOJ 2293) 동전 2 (0) | 2023.08.28 |



