트리

즉, 어떤 순환도 존재하지 않는 연결 그래프
트리의 성질
1. 순환 존재하지 않음
2. 유일한 루트 노드
3. 내차수가 0인 노드는 only 루트 노드, 나머지의 내차수는 1
트리의 용어
루트노드, 부모 자식노드, 터미널(리프 노드)는 제외
- 레벨
- 루트 노드의 레벨 = 0
- 어떤 노드의 레벨이 i일때, 자식의 레벨을 i+1
- 높이
- 정점들 중 최고의 레벨 (그래프 당 한 개)
- 정점의 차수
- 특정 정점의 부분 트리 개수 (유향, 무향 다 가능)
- 트리의 차수
- 모든 정점들의 차수 중 최대값
- n트리
- 모든 정점들의 자식이 최대 n개
- 리프 노드 외의 모든 정점들의 자식이 n개이면, 완전 n트리
- 예) 완전 이진트리
- 순서 트리
- 유향 그래프에서 같은 레벨에서 정점의 자식이 많을 때, 왼쪽부터 오른쪽으로 순서가 되어 있는 트리
- 숲
- 서로 연결되지 않은 트리들의 집합
- 부분 트리
- (T, v)는 v를 를 루트로 하는 부분 트리
트리의 활용 방안
- 파싱할때 그대로 사용
- 의사 결정 트리
- 가능성 있는 경우의 수를 효과적으로 표현하는 수단
레이블을 갖는 트리
: 각 정점을 점으로, 옆에 레이블 붙인 트리
- 선형의 산술식을 저장 할 수 있다.
산술식에서 마지막으로 연산되는 연산자를 "중심 연산자"라고 한다.
트리의 루트를 중심 연산자로 설정하여 트리를 구성해보자.

n 순서 트리의 유향 그래프 그리기
- 각 정점의 자식들이 n개라고 하고, 각 자식들의 순서에 대한 위치를 고정
- 집합 {1,2,3, ... , n}의 원소들로 레이블을 붙이되 고정된 위치(순서)에 맞는 원소를 골라 붙이기
- 이를 위치와 레이블을 갖는 유향 그래프라고 함.

최소 스패닝 트리
스패닝 트리란

- 구성 방법으로 DFS, BFS 등이 있다.
최소 스패닝 트리란

MST 찾는 방법
1. 프림 알고리즘
1. 최소 가중치 간선을 MST에 포함
2. 다음 정점에 연결된 간선 중 최소 가중치를 가지는 간선을 MST에 포함
3. 순회가 없도록 선정
2. 크루스칼 알고리즘
- 최소 가중치 순으로 순서 정한 뒤, 순환을 형성하지 않으면 그 간선 선택
트리 탐방 알고리즘
전위 표기법
1. 일반 전위 표기법
- 연산자 먼저 쓰고, 피연산자를 괄호로 묶어 표현
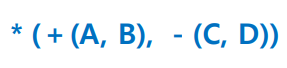
2. 케임브리지 폴란드식 표기법
- 일반 표기법에서 콤마 제거 후, 연산 기호도 괄호에 포함

3. 폴란드식 표기법
- 케임브리지 폴란드식 표기법에서 괄호 제거
- 가장 일반적인 반식

후위 표기법
= 역 포란드식 표기법
- 피연산자 먼저 쓰고, 그다음 연산자

중위 표기법
- 이진 연산에서만 적당
- 피연산자 사이에 연산자 표기

