https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
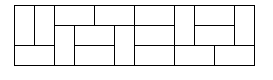
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.\
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
접근법
저번에 풀었던 2XN 타일링과 비슷한 문제이지만 생각해야할 점이 많다.
N=1인 경우부터 보자.
블록은 최소 2개부터 시작하므로 N=1은 나올 수 없다!
그다음 N=2인 경우를 보자

이렇게 총 3가지가 나온다.
N=3인 경우도 홀수인 경우 이므로 나올 수 가 없다!
N=4인 경우를 보자.
N=2d인 경우를 2개 붙여놓으면 되지 않을까?

그러면 정답은 9??
여기서부터 예외가 존재한다.
N=2인 경우(D[2])를 2개씩 붙여놓으면, 대칭적으로 나오게된다.
그러나 대칭이 아닌 모양이 존재한다.

위 경우는 따로 계산해야하기 때문에
D[4] = D[2]*3 + 2 = 11 이된다.
D[6]은 어떻게 될까?
(D[4]+D[2]) + (D[2]+D[4]) 로 계산하면 되나??
(D[4]+D[2]) , (D[2]+D[4]) 는 중복되는 경우가 포함된다.

중복되는 것 중 하나를 가져와봤다.
이를 어떻게 해결해야 할까?
정답은 대칭을 제거한 것만 포함시키면 된다.
아까봤던 특수문양은 대칭을 이루지 않기 때문에
D[4]+D[2] 를 한 다음, D[2]+D[4]를 특수 문양만 더해준다.
여기서 끝이 아니라, D[6]의 특수 문양을 추가로 더해야한다.
따라서 그림으로 표현하면 다음과 같다.

따라서, 점화식으로 표현하면
D[N] = D[N-2]*3 + {D[N-4]*2 + D[N-6]*2 + ... + D[0]*2} 로 표현할 수 있다.
코드
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
#define MAX 31
int main() {
int n;
int dp[MAX] = { 0, };
cin >> n;
dp[0] = 1;
dp[1] = 0;
dp[2] = 3;
for (int i = 4; i <= n; i += 2) {
dp[i] = dp[i - 2] * 3;
for (int j = i - 4; j >= 0; j -= 2) {
dp[i] += (dp[j] * 2);
}
}
cout << dp[n];
return 0;
}'📊알고리즘 > BOJ' 카테고리의 다른 글
| [👊DP뿌시기 #4] (BOJ 10844) 쉬운 계단 수 (0) | 2023.08.16 |
|---|---|
| [👊DP뿌시기 #3] (BOJ 14852) 타일 채우기 3 (0) | 2023.08.15 |
| [👊DP뿌시기 #1] (BOJ 11726) 2 X N 타일링 (0) | 2023.08.14 |
| [BOJ 1240] 노드사이의 거리 (0) | 2023.07.04 |
| [BOJ 2644] 촌수 계산 (0) | 2023.03.31 |


