728x90
https://www.acmicpc.net/problem/11779
11779번: 최소비용 구하기 2
첫째 줄에 도시의 개수 n(1≤n≤1,000)이 주어지고 둘째 줄에는 버스의 개수 m(1≤m≤100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스
www.acmicpc.net
접근 방법
1753 최단경로 문제에 경로까지 출력하는 짬뽕된 문제이다.
다익스트라를 이용하여 문제를 풀어보도록 하자.
기존 priority_queue를 이용한 코드에 경로를 저장하는 것이 이 문제의 핵심이다.
경로를 어떻게 지정할까 생각을 하다 최소신장트리에서 부모를 저장하는 방법을 사용해보기로 했다.
1. 부모를 저장할 parent[] 를 선언 (자기 자신으로 초기화)
2. 정점 i의 cost가 업데이트될 때마다 parent[i]를 업데이트한다.
3. 최단 경로를 구한 후, 목적지 B의 parent를 역추적한다.
예를 들어, 예제를 이용해 설명해보자.
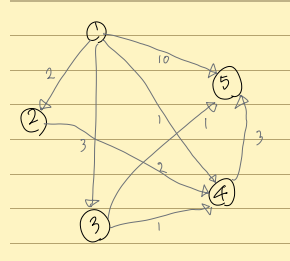
옆의 그림을 다익스트라를 따라 가며 보자.

1->2, 1->3, 1->4, 1->5 모두 1에서 진입하므로 1로 저장한다.
이후, cost가 update될 때마다 parent를 갱신한다.

최종 parent[]에서 parent[B] 부터 역추적하여 (parent[i] != i 일 때까지) 경로를 유추할 수 있다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <string>
#define MAX 1010
#define INF 987654321
using namespace std;
int n, m;
int a, b, w;
vector<pair<int, int>> nodes[MAX];
int parent[MAX];
int dis[MAX];
void dijkstra() {
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
dis[a] = 0;
pq.push(make_pair(0, a));
int cnt = 1;
while (!pq.empty()) {
int topDis = pq.top().first;
int topId = pq.top().second;
pq.pop();
//if (topId == b) break;
if (dis[topId] < topDis) continue;
for (int i = 0; i < nodes[topId].size(); i++) {
int oppo = nodes[topId][i].first;
int value = nodes[topId][i].second;
if (dis[oppo] > topDis + value) {
dis[oppo] = topDis + value;
pq.push(make_pair(dis[oppo], oppo));
// 갱신되면 부모 수정
//cout << "부모 갱신됨: " << topId << ", " << oppo << endl;
parent[oppo] = topId;
}
}
}
int curr = b;
vector<int> res;
res.push_back(curr);
while (parent[curr] != curr) {
cnt++;
res.push_back(parent[curr]);
curr = parent[curr];
}
cout << dis[b] << "\n";
cout << cnt << "\n";
for (int i = res.size()-1; i >=0; i--)
cout << res[i] << ' ';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++) {
cin >> a >> b >> w;
nodes[a].push_back(make_pair(b, w));
}
for (int i = 1; i <= n; i++) {
dis[i] = INF;
parent[i] = i;
}
cin >> a >> b;
dijkstra();
}
728x90
'📊알고리즘 > BOJ' 카테고리의 다른 글
| [그리디 #18] BOJ 11000 - 강의실 배정 (0) | 2024.02.22 |
|---|---|
| [그리디 #17] BOJ 21314 - 민겸 수 (0) | 2024.02.22 |
| BOJ 1753 - 최단경로 (0) | 2024.02.20 |
| [그리디 #16] BOJ 19598 - 최소 회의실 개수 (0) | 2024.02.19 |
| [그리디 #15] BOJ 1700 - 멀티탭 스케줄링 (0) | 2024.02.16 |



